Enabling exascale finite element simulations
After joining ICL in 2019, I have worked on two projects within the Exascale Computing Project (ECP): CEED and CLOVER.
For CEED, I primarily worked with the libCEED library, leading the effort to port the CUDA backends to HIP for AMD GPUs, as well as contributing to other GPU-related developments in the library. For CLOVER, I improved and expanded the interface of the MFEM finite element library to Ginkgo, enabling a minimal-overhead framework for interoperability between Ginkgo's solvers and preconditioners and those included in MFEM, as well as MFEM's matrix-free operators. (The podcast episode listed below discusses this interface in more detail.) I have also worked with porting the MAGMA linear algebra library to SYCL for Intel GPUs.
For both projects, I have been involved with efforts to investigate mixed-precision acceleration of simulations on GPUs. The following list gives an overview of the kind of work I have been involved in through ECP.


- Paper Three-precision algebraic multigrid on GPUs, Y. M. Tsai, NNB, and H. Anzt. Future Generation Computer Systems 149 (20 23). [journal link]
- Paper Mixed Precision Algebraic Multigrid on GPUs, Y. M. Tsai, NNB, and H. Anzt. Parallel Processing and Applied Mathematics: 14th International Conference, PPAM 2022, Revised Selected Papers, Part I (2023). [journal link] (winner of best workshops paper award)
- Podcast Enabling Cross-Project Research to Strengthen Math Libraries for Scientific Simulations, episode 95 of ECP's "Let's Talk Exascale" podcast (2022). [website link] [Apple podcasts link]
- Presentation Leveraging Mixed Precision to Accelerate High-Order Finite Element Methods on GPUs, NNB, J. Brown, J. Thompson, Y. Dudouit, and W. Pazner. SIAM Conference on Parallel Processing for Scientific Computing (PP) (2022).
- Paper libCEED: Fast algebra for high-order element-based discretizations, J. Brown, A. Abdelfattah, V. Barra, NNB, J-S. Camier, V. Dobrev, Y. Dudouit, L. Ghaffari, T. Kolev, D. Medina, W. Pazner, T. Ratnayaka, J. Thompson, and S. Tomov. Journal of Open Source Software 6(63) (2021). [journal link]
- Presentation MAGMA Backend and its Portability in Accelerating LibCEED using Standard and Device-Level Batched BLAS, NNB, A. Abdelfattah, S. Tomov, and J. Dongarra. SIAM Conference on Computational Science and Engineering (CSE) (2021).
- Paper High-Order Finite Element Method using Standard and Device-Level Batch GEMM on GPUs, NNB, A. Abdelfattah, S. Tomov, J. Dongarra, T. Kolev, and Y. Dudouit. IEEE/ACM 11th Workshop on Latest Advances in Scalable Algorithms for Large-Scale Systems (ScalA) (2020). [journal link] [UTK PDF link]
- Presentation Coupling MFEM with Ginkgo for efficient preconditioning on GPUs, NNB, T. Kolev, W. Pazner, H. Anzt, T. Grützmacher, P. Nayak, and T. Ribizel. CEED 4th Annual Meeting (2020).
HPC for HPS
Work with my postdoc advisor, Adrianna Gillman.
The Hierarchical Poincaré-Steklov (HPS) method is a discretization technique based on domain decomposition and classical spectral collocation methods. It is accurate and robust, even for highly oscillatory solutions. An associated fast direct solver is built from hierarchically merging Poincaré-Steklov operators on box boundaries and storing the necessary information; the solve stage then involves applying the operators in a series of small matrix-vector multiplications.
We worked on parallelizing, optimizing, and accelerating the algorithm, especially the build stage. Our 2D shared memory parallelization technique reduced the build stage times from approximately 10 minutes to approximately 30 seconds for over 3 million unknowns.
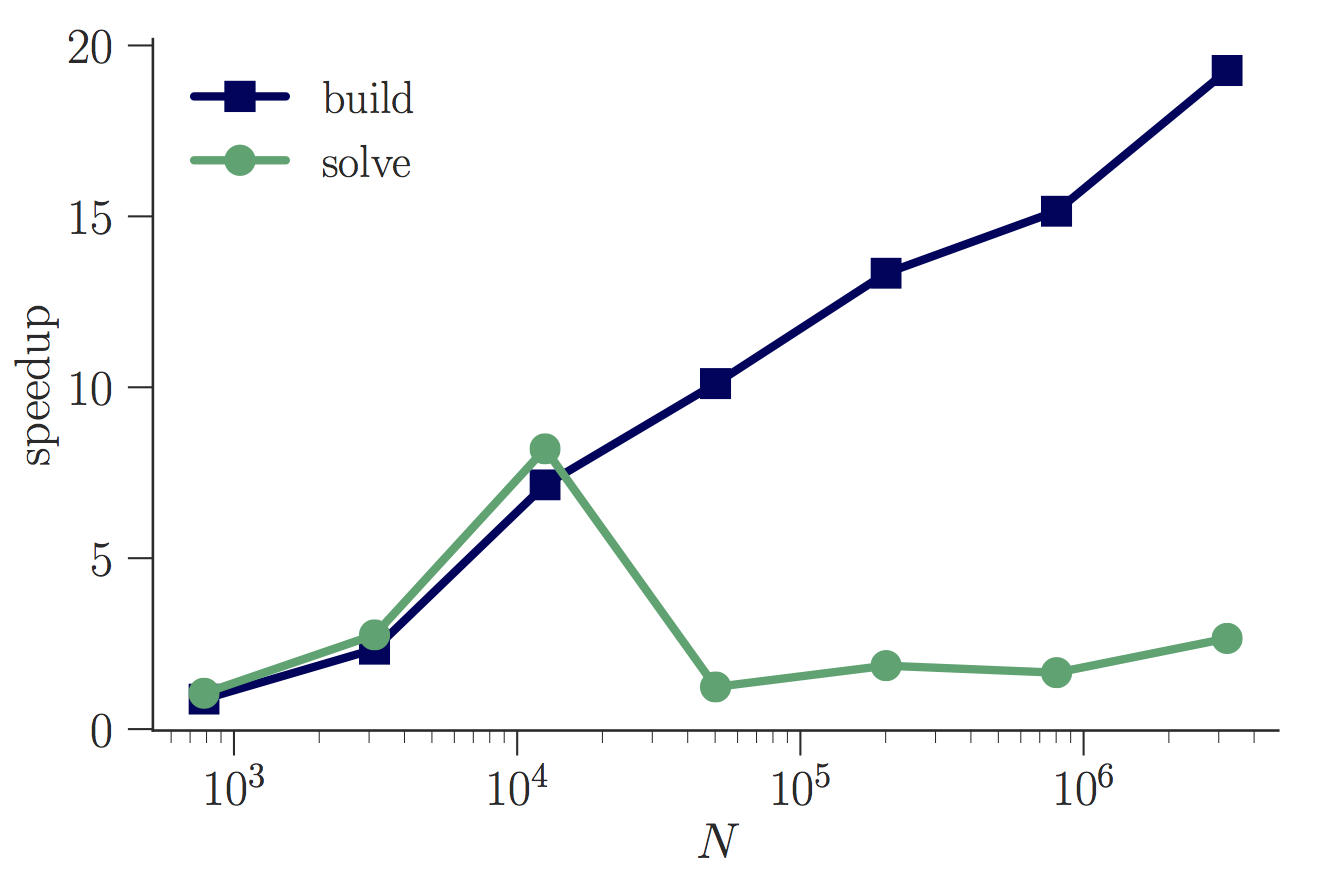
- Paper A parallel shared-memory implementation of a high-order accurate solution technique for variable coefficient Helmholtz problems, NNB, A. Gillman, and R. Hewett. Computers and Mathematics with Applications 79(4) (2020). [journal link] [arXiv link]
- Presentation An Efficient and High Order Accurate Solution Technique for Three Dimensional Elliptic Partial Differential Equations, NNB and A. Gillman. SIAM Conference on Computational Science and Engineering (2019).
- Presentation A Parallel Implementation of a Hierarchical Spectral Solver for Variable Coefficient Elliptic Partial Differential Equations, NNB, A. Gillman, and R. Hewett. International Conference on Spectral and High Order Elements (2018).
- Presentation A parallel implementation of a high order accurate variable coefficient Helmholtz solver, NNB, A. Gillman, and R. Hewett. SIAM Conference on Applied Linear Algebra (2018).
- Poster A parallel implementation of a high order accurate variable coefficient Helmholtz solver, NNB, A. Gillman, and R. Hewett. Rice Oil & Gas HPC Conference (2018).
FE-IE for interface problems & irregular domains
We developed and implemented a new, high order finite element-integral equation coupling method for elliptic interface problems. The method leverages the strengths of FE and IE methods to handle different aspects of the problem. It can handle general jump conditions at the interface, and the jump conditions appear only in the right hand side of the system to be solved. Additionally, the method does not suffer from loss of convergence order near the boundary when the boundary is smooth and the problem data can be extended as necessary across the interface. It also doesn't require the construction or use of any special basis functions; in fact, much of the standard machinery for both the FE and IE solvers can be used, simplifying implementation from a software standpoint.

- Paper High-order Finite Element—Integral Equation Coupling on Embedded Meshes, NNB, A. Klöckner, and L. N. Olson. Journal of Computational Physics 375 (2018). [journal link] [arXiv link]
- Presentation Targeting Interface Problems at Scale with Coupled Elliptic Solvers, NNB, A. Klöckner, and L. N. Olson. 6th Joint Laboratory for Extreme-Scale Computing Workshop (2016).
FE-based P3M
The goal of this project was to create an FE-based version of the particle-particle–particle-mesh (P3M) methods for N-body problems. P3M methods separate particle interactions into short-range (only required for near neighbors) and far-field (smooth, and solved easily on a mesh with your favorite numerical method). A common choice is to achieve the P-P/P-M splitting through Gaussian screen functions (as in the classic Ewald sum) and solve the mesh problem with FFTs.
We developed a method which constructs special polynomial screen functions out of finite element basis functions. Thus the screens are represented exactly on the finite element mesh, removing several possible sources of error in a finite element solution to the mesh problem. Indeed, we aimed to make the mesh problem especially suited to being solved with finite elements, avoiding the geometry restrictions and parallel communication burdens of the FFT.
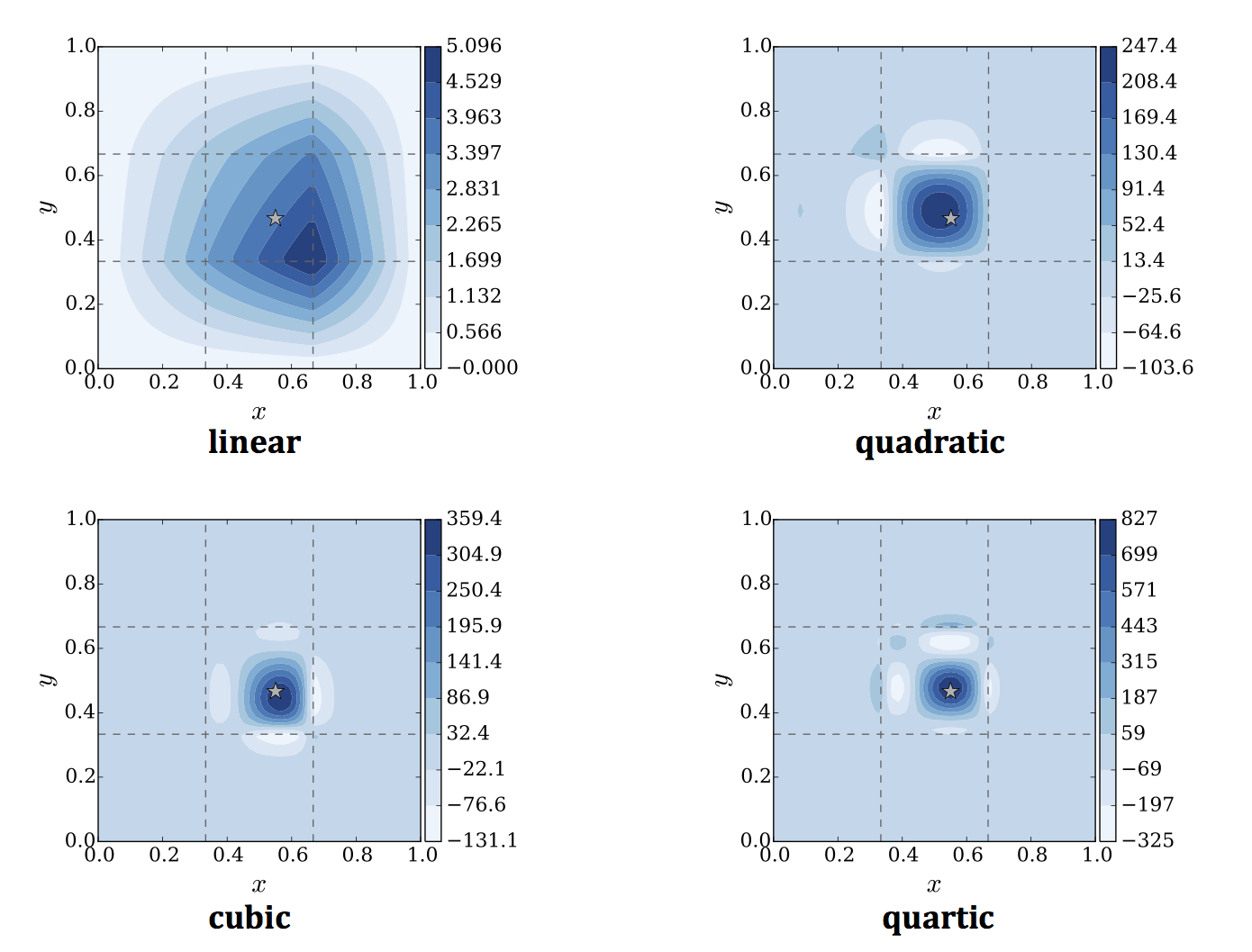
- Paper A Finite Element Based P3M Method for N-body Problems, NNB, L. N. Olson, J. B. Freund. SIAM J. Sci. Comput., 38(3) (2016). [journal link] [arXiv link (slightly older version)]
- Poster A Method for N-Body problems based on Exact Finite Element Basis Screen Functions, NNB, L. N. Olson, and J. B. Freund. SIAM Conference on Computational Science and Engineering (2015).
- Presentation A Scalable Method for Cellular Blood Flow and Other N-body Systems, NNB, L. N. Olson, and J. B. Freund. University of Illinois at Urbana-Champaign Computational Science & Engineering Annual Meeting (2013). [video]
Other
- Presentation Ordered and chaotic flow of red blood cells flowing in a narrow tube, NNB and J. B. Freund. 66th Annual Meeting of the American Physical Society Division of Fluid Dynamics (2013).
- Presentation Stability of red cells flowing in narrow tubes, NNB and J. B. Freund. 64th Annual Meeting of the American Physical Society Division of Fluid Dynamics (2011).
- Presentation Program Visualization Tool for Educational Code Analysis, NNB. 2010 Global Conference on Educational Robotics (2010). [Do you like educational robotics? Then you should check out the awesome people who run GCER and their Botball program]